楕円曲線論はじめの一歩 (4)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回は、時計の短針を例に、有限巡回群について語りました。
有限巡回群について、もう少しだけ、お話しておくことがあります。

群の位数、元の位数

群に含まれる要素の数を、「群の位数」と呼びます。
前回触れた時計の短針の場合、群の位数は 12 です。
なぜなら、要素（元、つまり時刻）は 12 種類あるからです。

こちらは簡単ですね。

また、「その元を何回足し合わせると単位元になるか？」という値を、
「元の位数」と呼びます。

こちらは少し難しいので例を挙げましょう。

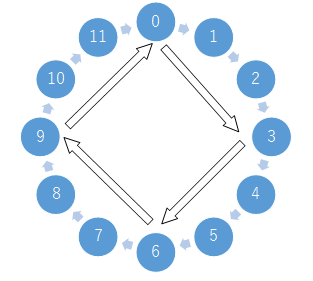
3 は、単位元（0）から 4 回足すと、元の単位元に戻ってきます。

だから、元 3 の「元の位数」は 4 となります。

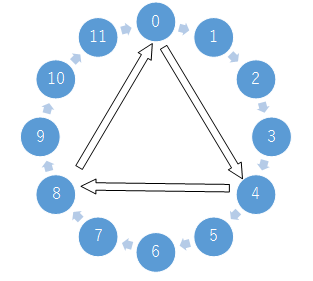
4 の場合を見ると、3 回足すと単位元に帰ってきます。
だから、4 の「元の位数」は 3 です。

群の位数と元の位数の関係

それぞれの元に対する、元の位数を表にしてみましょう。
単位元 0 は既に単位元に戻っているため、省略します。

元	元の位数
1	12
2	6
3	4
4	3
5	12
6	2
7	12
8	3
9	4
10	6
11	12

すべて 12 の約数であることにお気づきでしょうか？

そう、有限巡回群においては、どの元の位数も、群の位数の約数になるという法則があります。
証明は今回も省略します。

素数位数の群

「元の位数」は「群の位数」の約数であるというお話をしました。
ということは、群の位数が素数、例えば 7 ならばどうでしょう？

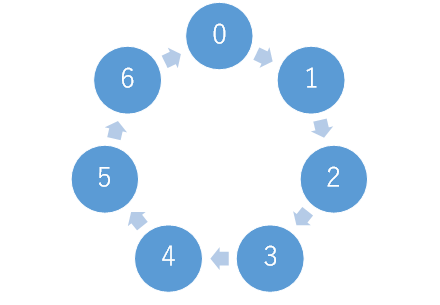
また表にしてみましょう。

元	元の位数
1	7
2	7
3	7
4	7
5	7
6	7

「群の位数」が素数であるということは、約数は「群の位数」それ自身か、1 しかありえません。
ということは、必然的に全ての元の位数は、群の位数に一致します。

「ラグランジュの定理」と呼ばれる性質です。

まとめ

今回は、群の位数と元の位数についてお話しました。
そして、ラグランジュの定理にも少し触れました。
大事な性質なので、よく覚えておいてください。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。