はじめに
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、吉川です。
今回はVIPPOOLが販売している世界最高水準の性能を誇る
アルトコイン向けマイニングボード「VMINE」を使用してみる記事です。
VMINEの外観

箱から本体を取り出しました。付属品はありません。2つのファンの下にヒートシンクがあります。直接見ることはできませんが、ヒートシンクの下にマイニングチップが並んでいます。ヒートシンクの脇には電源供給や通信のための端子があります。
このボードはPCIeカードの形状をしているので、グラフィックカードと同様に市販のマイニングリグ筐体に取り付けることが可能です。

上側側面には電源端子と複数枚接続用端子があります。

ブラケット面にはmicro-USB端子があります。写真は試作品のためリセットスイッチがありますが、製品にはありません。
マイニングの準備
さっそくマイニングの準備をしていきます。今回はマイニングリグに組み込まず、卓上に平置きするので、ボード裏側に市販のゴム足(タカチ電機工業 B26-11)を取り付けました。

続いて電源とUSBケーブルを接続します。今回は市販のATX電源(Seasonic SSR-850FX)を使用しました。
これで接続は完了です。電源ユニットのスイッチをONにすると、システムが動作していることを示すボード上のLEDが点滅し、ファン(光らない)が回転し始めます。

次にマイニングソフトウェアを準備します。
配布されているファイル一式をダウンロードし、ドライバをインストールします。
マイニング
マイニングには VMINE 用にカスタムされた専用マイニングソフトウェア、vminer を使用します。
使用するアルゴリズムや接続するプール等を指定して vminer を起動するとマイニングが始まります。
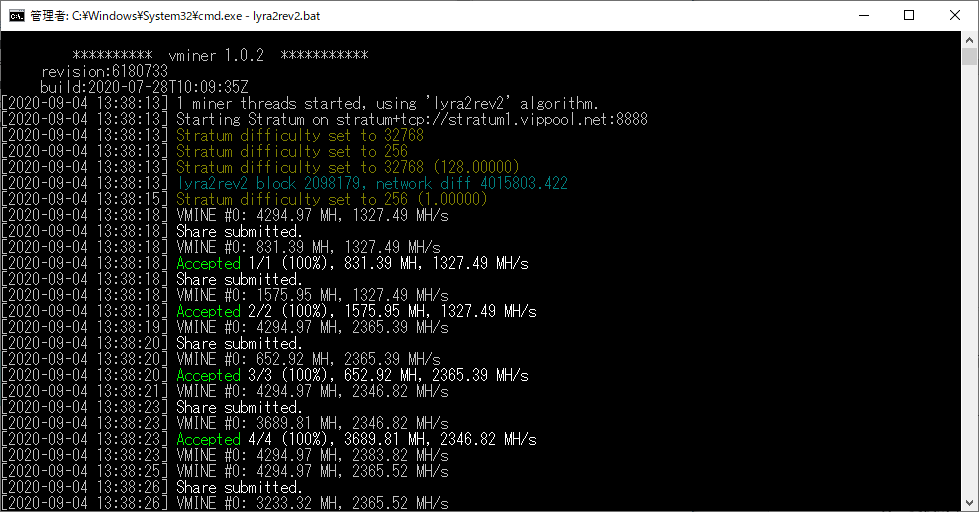
あとはこのまま放置するだけです。コンソール画面には現在のハッシュレートが表示されており、ほぼ公称値と同じ値が出ています。
ファンは過不足なく冷却するよう制御されており、卓上に置いていても極端にうるさいとは感じません。
マイニングを開始して10分ほど経過した状態の消費電力は176Wでした。今回使用した電源は80 PLUS GOLDなので、消費電力も公称値どおりと言えるでしょう。

おまけ
VMINE はボード同士を複数枚接続して、マイニング能力を増強することができます。
VMINEを複数枚購入するとボード間接続用の専用ケーブルが付属します。
試しに2枚目のVMINEを接続してみました。

VIPPOOLのコンソール画面からもハッシュレートを確認できます。約 350W でこのハッシュレートですから電力性能は GPU より格段に良いです。

まとめ
VIPPOOL が発売している世界最高水準の性能を誇るアルトコイン向けマイニングボード「VMINE」を試してみました。
ケーブル2本の接続とドライバインストールだけで、ASICマイニングが楽しめます。
私は次の冬にVMINEを暖房代わりにして暖を取ろうと企んでいます。
暖房として使う場合は消費電力が大きくなるlyra2zでマイニングするのがおすすめです。
ご質問、ご意見等ありましたらお気軽にリプライください。
