今回のおはなし
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、星月です。
前回は「足し算」とは何か。つまり「群」について語りました。
今回は、「モノの個数」以外にも「群」の条件を満たすものがあるので、
それについて見ていきましょう。
時計の短針、実は群
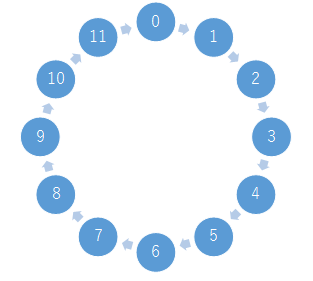
これは 1 時間に 1 つずつ進んでいく時計の時針です。
モノの個数ではないですが、これも実は群の条件を満たしています。
1 つずつ確認してみましょう。
演算に対して閉じている
1 時から 1 時間経つと 2 時。
3 時から 4 時間経つと 7 時。
8 時から 6 時間経つと 14 時...かと思いきや 2 時。
ちゃんと演算に対して閉じていますね。
逆元
3 時の 3 時間前は 0 時。
5 時の 5 時間前も 0 時。
逆元はきちんと存在しています。
記号の世界の言葉で説明してみる
今の短針の位置、つまり 0 時からの経過時間を x、追加する経過時間を y としましょう。
この時計の短針の位置は で計算できます。
mod は剰余、つまり「あまり」のことで、x と y を足して、12 で割ったあまりが、
新しい短針の位置になります。
このように、ぐるっと回って元に戻る構造をしている群のことを「巡回群」と呼び、
特に「巡回群」の要素となっている元の個数が有限であるもののことを「有限巡回群」と呼びます。
数学の世界では、12 個の要素からなっている有限巡回群を と書いたりします。
まとめ
モノの個数以外にも、群の条件を満たすものがあり、
その一例を見てみました。
今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。