今回のおはなし
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、星月です。
前回、楕円曲線上の有理点は、可換群であるというお話をしました。
可換群であるということがわかると、次に気になるのはその位数や構造です。
今回は楕円曲線上の有理点がなす可換群の構造について見ていきましょう。
今回の話は、私が楕円曲線について勉強したとき、
「これすごくない!?」と感動したところなので、
この感動をぜひ皆さんとも共有したく思います。
正直に言うと、この話が書きたくて、この連載をしていると言っても過言ではないくらいです。
楕円曲線上の有理点がなす可換群と、複素平面との、切っても切れない関係
昔むかし、ヴァイエルシュトラスさんが発見しました。
楕円曲線 の係数、a と b から上手いこと計算すると、
複素数 と
を求めることができます。
この 2 点を複素平面上に置きます。
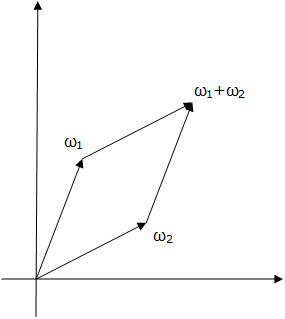
すると、0 と 、
、
の 4 点で
平行四辺形を作ることができます。
ヴァイエルシュトラスさんは、この平行四辺形の中の複素数と、
楕円曲線上の有理点がなす可換群が一対一で対応づけできる。
ということを発見しました。
これだけじゃピンとこないと思うので、具体例をあげていきたいと思います。
位数 2 の点と対応する複素数
楕円曲線上の有理点の個数は未解決問題なので、
可換群の「群の位数」は不明です。
ですが、「元の位数」ならわかるものはいくつかあります。
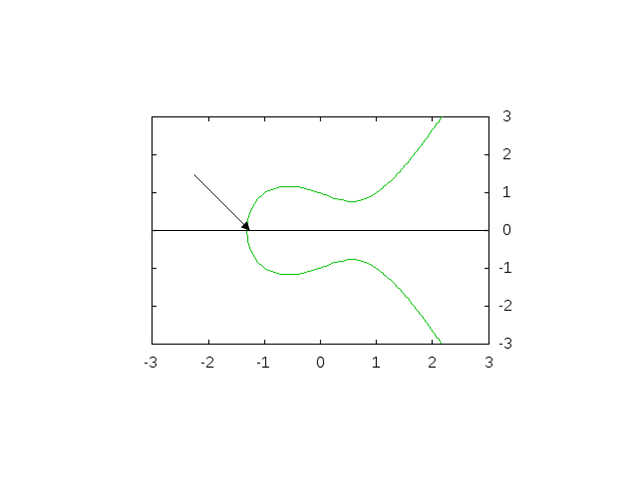
例えばここ。x 軸との交点。P と名づけましょう。
ここが有理点の場合、傾きは垂直なので、
接線は当然、垂直線になります。
ということは、P+P= と無限遠点になるため、
| P | P |
| P+P | O |
| P+P+P | P |
| P+P+P+P | O |
というわけで、元の位数が 2 の有理点であることがわかります。
さて、複素平面に戻りましょう。
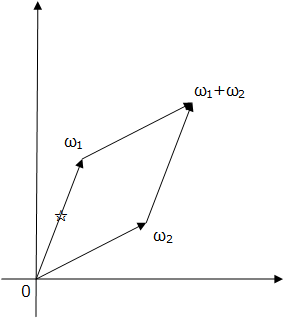
☆マークを打ちました、 の点が、有理点 P と対応します。
先ほどお話した通り、有理点 P の「元の位数」は 2 だったので、
P+P=
でした。
複素平面で対応する点を計算してみましょう。
はい、平行四辺形の交点にたどり着きました。
どうでしょう?
2 倍すると無限遠点になる有理点 P と対応する複素数 も、
2 倍することで無限遠点と対応する複素数 になるわけです。
楕円曲線上の有理点と、複素平面上の点とが対応しているだけでなく、
「楕円曲線上の有理点の加算は、複素数の加算と対応している」ことがわかるでしょうか?
今回は元の位数が 2 の点で試しましたが、他の位数の点でやっても、
同じようなことが言えます。
これ、すごくないですか?
すごいですよね??
楕円曲線上の有理点と複素平面上の点(複素数)とが対応しているだけではなく、
有理点同士の加算と、複素数の加算がちゃんと対応しているというわけで、
この 2 つの群は本質的に同じ構造を持っている、という主張ができるわけです。
端的に言ってすごいと思います。