今回のおはなし
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、星月です。
前回まで、代数論の基礎を簡単になぞりました。
そして今回からみなさんお待ちかね、楕円曲線の話をはじめようと思います。
楕円曲線って何でしょう?
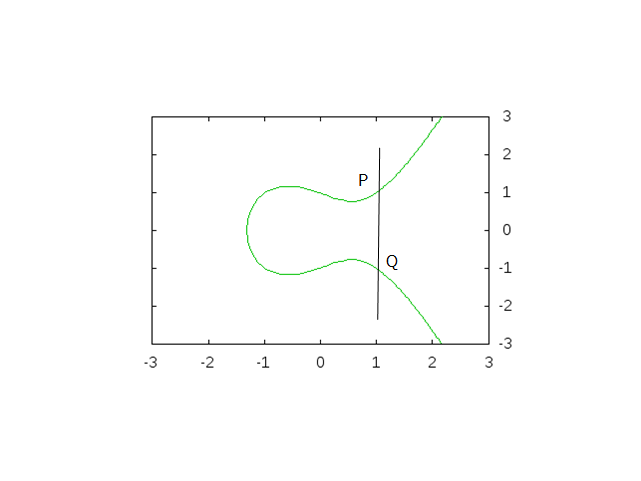
楕円曲線とは、 こんな形をした方程式のことです。
こんな形をした方程式のことです。
a, b は係数で、x と y が変数です。
この方程式の解をグラフにするとこんな感じになります。
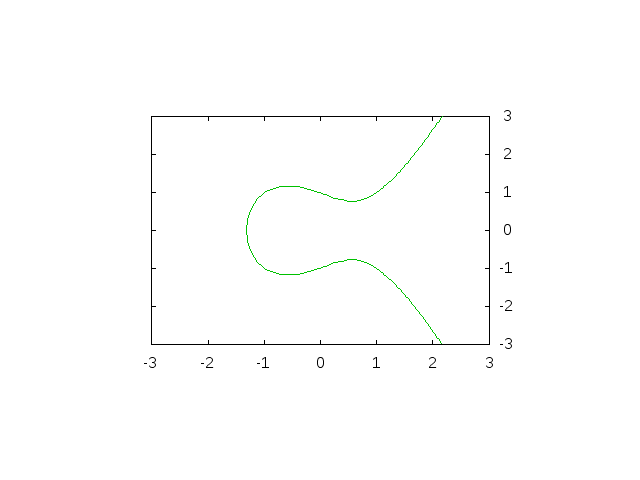
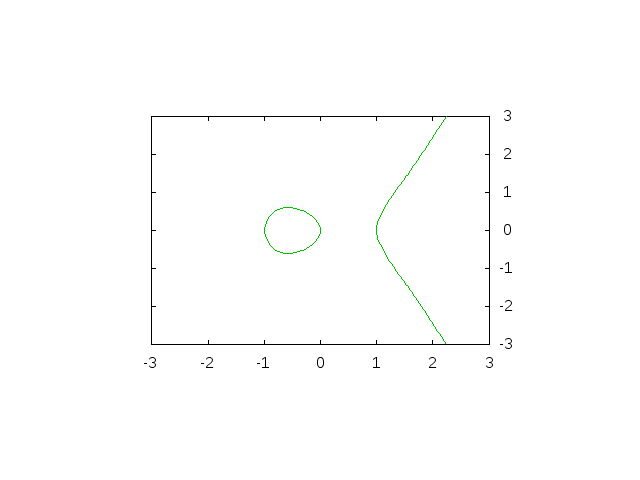
え、どのあたりが楕円かって?...名前のことは気にしない方がいいです。
いろいろな歴史的事情でこう呼ばれているだけで、これが楕円曲線なんです。
詳しく知りたい方は、楕円積分について調べるといいですが、
あまりオススメはしません...
天下り的で申し訳ないですが、こればかりは、「こういうもの」として
覚えていただければと思います。
さて、問題です。
ある楕円曲線が与えられたとき、その楕円曲線に含まれる有理点、
つまり x, y 座標それぞれが有理数となる点はどれだけあるでしょうか?
まったく存在しない?それとも有限個?もしくは無限に存在する?
...実はこの問題は未解決問題の 1 つで、未だに回答は出ていません。
残念。
楕円曲線上の有理点を探す問題
未解決の問題について考えても仕方ないので、
とりあえず、さらに条件を加えます。
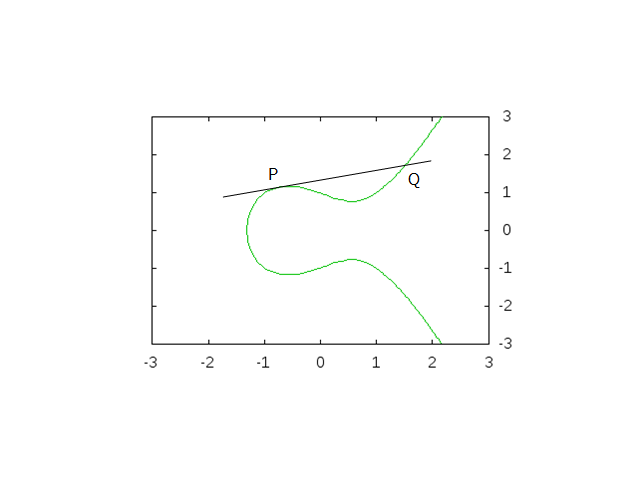
ある楕円曲線と、「その楕円曲線上の有理点が 2 つ与えられたとき」、
他の有理点を探すことはできるでしょうか?
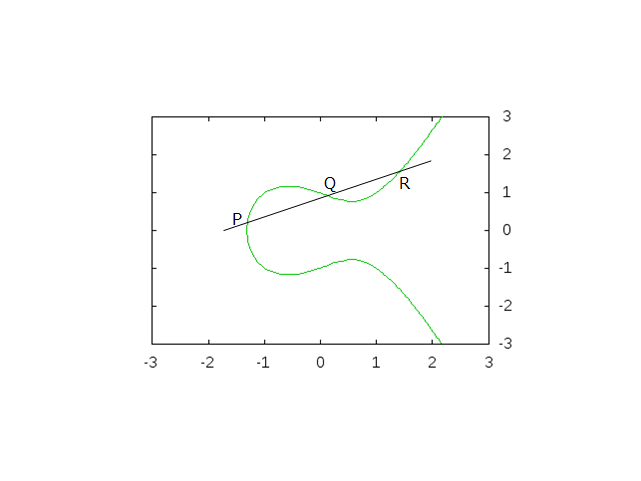
実は、楕円曲線に交わるように直線を引くと、その直線は必ず 3 箇所で交わります。
実際には例外があって 2 箇所になる場合もありますが、とりあえず後回しにします。
この交点を左から順に P, Q, R としましょう。
P と Q が有理点であれば、R も有理点になることは計算すればわかります。
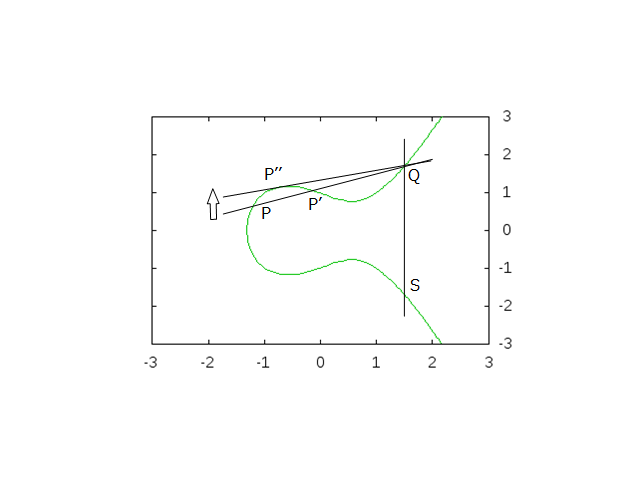
これだけだと、3 つ目を見つけて終了してしまいますので、さらにもう 1 つみつけましょう。
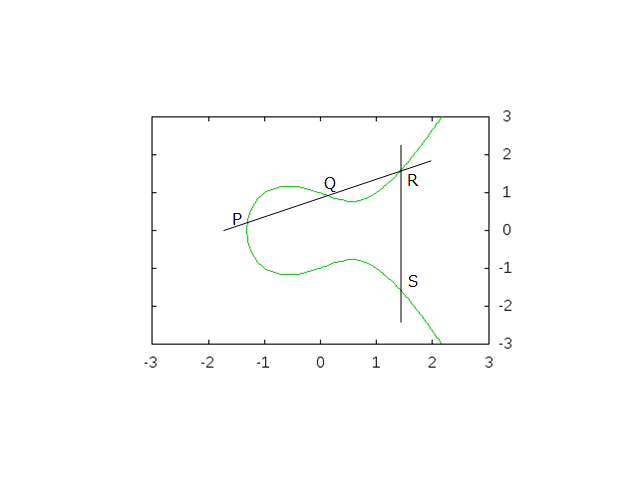
R を通る垂直線との交点、つまり、R の y 座標を反転させた点 S も有理点となります。
( x, y ) が有理点なら、 ( x, -y ) も有理点、という話です。
さて、これで 4 つ目が出てきました。ここで、直線 SP や直線 SQ を引くと、
さらにたくさん有理点が見つかりそうですね。
点 S を導き出せるのは非常に重要そうです。
さて、ここで、つまり有理点は無限に存在するんだ!と思ったあなた、残念早とちり。
これを繰り返したときに、既知の点以外である保証がないので、
無限に存在するとは限りません。つまり、どこかでループする可能性があるのです。
ともあれ、2 つの有理点から、別の有理点を見つける方法があることはわかっていただけたと思います。
実際に計算してみる
有理点 P の座標 ( x1, y1 ) と、有理点 Q の座標 ( x2, y2 ) から、新たな有理点 S の座標 ( x3, y3 )
を求めてみましょう。
詳しい計算については他のサイトを参照してもらうことにしてここでは答えだけ。


と、なります。x1, x2, y1, y2 すべて有理数ならば、x3, y3 も有理数になることがおわかりでしょうか?
有理点 2 つから、新たな有理点が得られることが、数式からも見て取れます。
まとめ
今回からようやく楕円曲線の話に入りました。
話題の焦点は「楕円曲線上で、x と y がともに有理数となる点」つまり「有理点」です。
これを突き詰めていくと面白いことがたくさんあります。
今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。