今回のおはなし
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、星月です。
前回は、楕円曲線と直線が 2 点で交わる場合について見てみました。
実はもう 1 パターン、2 点でしか交わらないケースがあるので、
今回はそちらについて見てみましょう。
垂直線になる場合
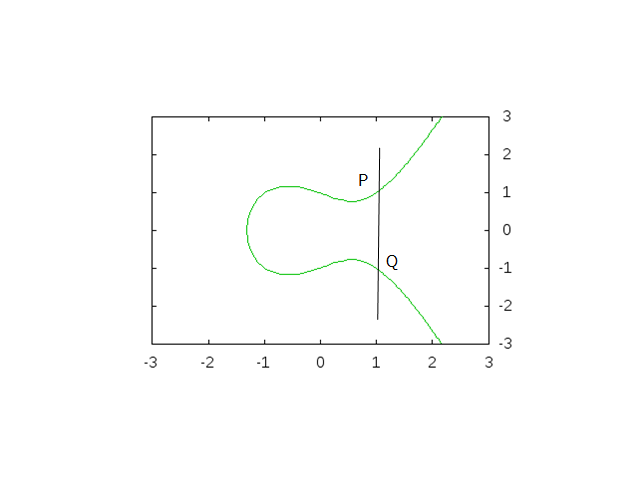
これはつまり、( x, y ) と ( x, -y ) が与えられた場合ですね。
この場合は完全な垂直線を引くことになり、2 点でしか交わりません。
そこで、「無限遠点」という概念を持ってきます。
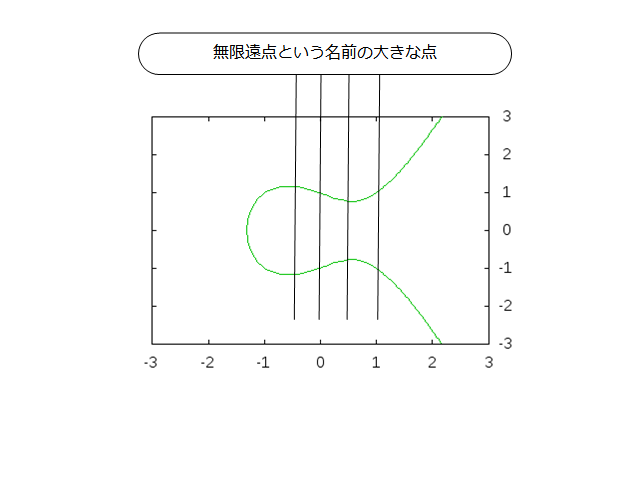
グラフの上の方(下の方でもいいですが)には、「全ての垂直線と交わる点がある」と考えます。
少し突飛な考え方ですね。
地球儀の、北極点を想像してみてください。
北極点は、地球上の全ての経度線と交わっていますね。
そんな感じです。
二次元のグラフで見ていると少し滅茶苦茶に見えますが、
実は射影平面という考え方を導入して三次元で見ると実在する点なのです。
射影平面
ここで、楕円曲線の定義を思い出してみましょう。
ここで、今は有理点、つまり x と y が有理数である点について考えているので、
有理数は 2 つの整数を使って と表すことができるため、
と書くことが出来ます。大文字で書いた X, Y, Z は全て整数です。
両辺に をかけてやると、
となります。どの項も、X, Y, Z をあわせると 3 次の項になっていることがお分かりでしょうか?
a と b は楕円曲線を定義するパラメータで、定数なので次数にはカウントしません。
このように、全ての項の次数が同じ方程式のことを、同次式と呼びます。
変数が 3 つに増えたので、三次元のグラフを想像してみましょう。

このように、3 次元の空間でみると、Z=1 のところでスライスした断面図が、
今まで見てきた楕円曲線のグラフであることは、数式からわかると思います。
次元が 1 つあがっているので、楕円曲線上の点は、この空間内での線(実際には「整数」に限定してるので点線)
になり、楕円曲線自体は面(整数に限定してるのでメッシュ状の面)に対応していることになります。
2 つの点を結ぶ直線も面に対応しているので、楕円曲線の面と重なっている曲線が、交点を表すことになります。
では無限遠点はどこに対応するのでしょうか?

それはここ。Z=0 の平面です。
グラフ上でどの垂直線をとっても、この三次元空間で見ると Z=0 の面と交差していることにします。
というわけで、二次元では描けない点が実は存在している、ということで
理解しておいていただければと思います。
ちなみに、無限遠点は と表記することが多いようです。