今回のおはなし
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、星月です。
前回、「楕円曲線に交わるように直線を引くと、その直線は必ず 3 箇所で交わります」と書きましたが、
実際には例外があります。
今回はその例外について見ていきましょう。
楕円曲線と接する場合
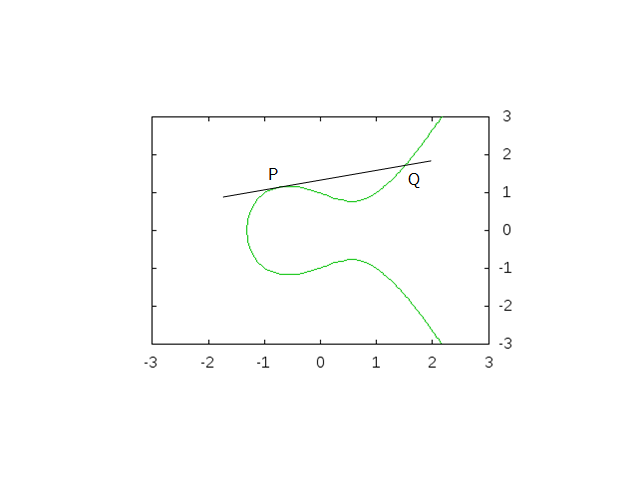
楕円曲線に直線を重ねると、この図のように接線となる場合があります。
その場合は、2 点でしか交わりません。
このような場合は、3 点で交わっている状態から連続的に変化させていき、その極限を考えます。
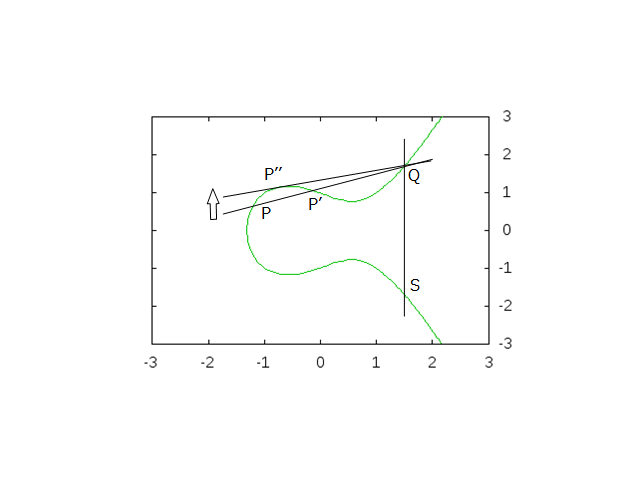
P-P'-Q の直線は 3 点で交わっています。
これを少しずつ、Q の位置を変えずに上にずらしていきます。
すると、P と P' はどんどん近づいていって、あるとき P'' の 1 点に集約されます。
つまり、接線となっている点は、その点で 2 回、交わってる状態と「連続」しているわけです。
要するに、接線の部分で 2 回交わっているとカウントするわけですね。
中学校で二次方程式の解を求める時に、「重解は 2 回交わっているものとみなす」と習いました。
あれと同じです。
数式で考えるともう少し明白です。
前回、2 点 P = ( x1, y1 ) と Q = ( x2, y2 ) から有理点 S を求める式をお見せしました。
ここで、 を考えます。
x2 が変化すると y2 もあわせて変化していくことに注意して極限を求めると、
が得られます。今回も詳細な計算は省略します。
式の形はだいぶ違いますが、傾きを表している
が、
に変わっているだけです。
直線を連続的に移動させて点 P と点 P' が極限まで近づいて点 P'' になる。
これを数式で考えるとこうなる、というお話です。
接する場合を考えると何ができるか
さて、以上の考え方を逆にすれば、
「楕円曲線上に有理点が 1 個があれば、そこに接線を引くことで別の有理点が見つかる」
ということになります。
P と P' から S を発見できるのであれば、P'' と P'' からも S を発見できるというわけです。
前回は有理点が 2 個から別の点を見つけましたが、実は 1 個でもあれば見つけられる、
というお話です。
まとめ
今回は、楕円曲線と直線が 3 点で交わらないケースについて見てみました。
実はもう 1 パターンあるのですが、それについては次回、触れることにしましょう。
今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。