はじめに
みなさんこんにちは。
VIPPOOL でエンジニアをやっています、星月です。
今回は、bitcoin や monacoin など、主要な暗号資産で使われている、
楕円曲線暗号について、少しお話ししようと思います。
みなさんは、楕円曲線暗号についてどのように感じていますか?
「なんかよくわからないけど強そう」「普通の暗号より強いって聞いた」
そんな感じの印象を持っている方に、読んでいただきたい記事です。
暗号技術概論
暗号には、暗号化と復号で同じ鍵を使う対称鍵暗号(共通鍵暗号)と、
双方で異なる鍵を使う非対称鍵暗号の二種類があります。
共通鍵暗号としては、有名なところでは AES, 3DES などがあります。
非対称鍵暗号と比べると、「共通で使う鍵をどうやって安全に共有するか」
という問題があるものの、非常に演算が軽い、というメリットがあり、
現在でもよくつかわれています。
一方、非対称鍵暗号は、鍵が二種類存在するもののことで、
演算が重いというデメリットがありますが、
鍵を共有する手間がないというメリットを生かして、ただの暗号化以外にも、
電子署名などの応用がされています。暗号資産で使われているのも、
この電子署名の技術です。
旧世代の非対称鍵暗号
非対称鍵暗号では、ほとんどのものは離散対数問題が困難な有限巡回群を使います。
有限巡回群や、離散対数問題については、以前このブログで解説いたしましたので、
詳しくはそちらをご覧ください。
- 有限巡回群の話 楕円曲線論はじめの一歩 (3) - VIPPOOL開発者ブログ
- 離散対数問題について 楕円曲線論はじめの一歩 (14) - VIPPOOL開発者ブログ
さて、かつて、非対称鍵暗号が実用化された時には、有限体乗法群が使われていました。
有限体 や、その拡大体
での演算、
で、体のパラメータ p, n, b をパラメータとして公開し、
x を秘密鍵、y を公開鍵とする方法です。x と、パラメータの p, n, b から、
y を計算するのは簡単ですが、y とパラメータから x を計算するのは非常に難しい、と。
楕円曲線暗号の登場
ところが、この技術が普及するにつれて、y から x を計算する手法について、
様々な研究が行われてきました。現在では、それなりに効率のよい手法が発見されています。
そこで登場するのが、楕円曲線上の群です。
既存の暗号アルゴリズムで使っていた有限体乗法群を、そっくりそのまま、
楕円曲線上の群に入れ替えたものが作られました。
例えば、DH 鍵交換アルゴリズムの楕円曲線バージョン、ECDH や、
ElGamal 暗号の楕円局背バージョン、EC-ElGamal、
DSA の楕円曲線バージョン ECDSA などです。
これらが、いわゆる楕円曲線暗号です。
暗号資産では、ECDSA を使用しているものが多いです。
楕円曲線暗号の強さ
各種暗号アルゴリズムの強さについては、米国の NIST という組織が調査しています。
今回は、そこの公開している SP800-57 という文書から引用してきます。
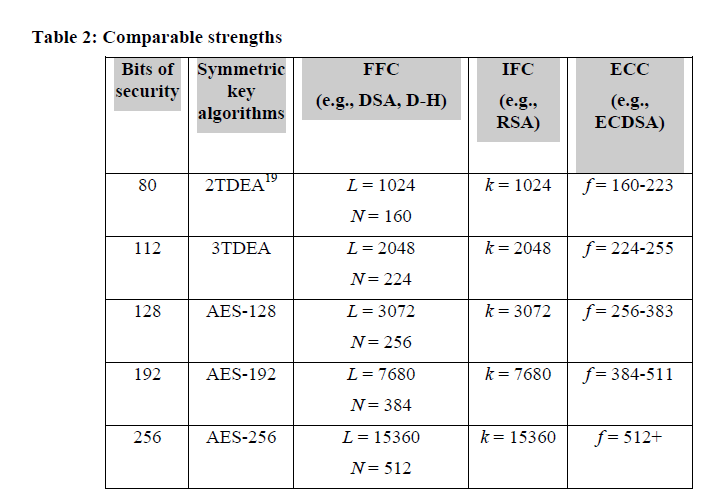
この表で、左端が暗号の強度、AES を基準に何ビット相当の強さなのかを示した数字です。
真ん中の FFC が、有限体乗法群を用いた暗号で、L がいわゆる鍵長です。
また、ECC が楕円曲線暗号で、f が鍵長です。
これを見るとわかる通り、有限体乗法群の 1024bit が、楕円曲線暗号の 160-223bit と同様で、
AES の 80bit 程度の強度というわけで、つまり「同じ強度で比べたら短いビット数で済む」
ということを示しています。
ただ、これは実は単純に楕円曲線の演算が重いため、総当たりにかかる時間が長い、という
ことを示しているだけで、「暗号として強い」ではなく「計算が重い」ことを示しているに過ぎません。
では、どこが強いのか。
この表をグラフにしてみてみましょう。

横軸(上)が楕円曲線暗号の鍵長で、横軸(下)が有限体乗法群の鍵長です。縦軸が暗号の強さです。
これを見るとわかる通り、楕円曲線暗号は、暗号強度と鍵長が比例するように伸びていきますが、
有限体乗法群では、だんだん上がり方が鈍くなっています。
これこそが、「効率的な解き方が発見された」ということであり、
まだそれが見つかっていない楕円曲線暗号が強いと呼ばれる所以です。
つまり、今後、コンピュータの技術が進歩して計算能力が高くなっていくとします。
そうすると、当然、それに合わせて安全とされる暗号強度も高くなるわけですが、
楕円曲線暗号では比例して鍵長を伸ばせば済みますが、有限体乗法群では、すごい勢いで
鍵長を増やす必要があります。
例えば、先ほどの表に戻って、暗号強度 256bit 相当の強度が必要な時代になったとき、
楕円曲線暗号では鍵長 512bit で済みますが、有限体乗法群でその強度を実現するには、
15360bit もの長さが必要になるということです。
どうでしょう?これが、楕円曲線暗号が「強い」と言われる意味です。
まとめ
今回は、楕円曲線暗号が「強い」と言われる理由について、
簡単にお話ししました。
ただ単に、短い鍵長で同じ強度、という単純な話ではなく、
将来を見据えたときに安全性の高いものだ、というところを、
しっかりと押さえていただければと思います。
今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。