楕円曲線論はじめの一歩 (14)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回は、楕円曲線上の有理点がなす群が、有限巡回群である、というお話をしました。

「楕円曲線論」としてはこのくらいにしておいて、
そろそろ「楕円曲線暗号」に応用していくお話をして、
この連載を〆ようかと思います。

有限体上で定義される楕円曲線

これまで、楕円曲線は暗黙のうちに実数上で定義して、
その中の有理点について見てきました。

つまり、x 座標、y 座標ともに実数で考えれば、グラフに滑らかな曲線を描けるし、
その中で x 座標と y 座標がともに有理数になる点についてのみ考えてきたわけです。

これまでの知見を楕円曲線暗号として活用しようとすると、
コンピュータでは真の意味での実数は扱えないし、
有理数は桁が無限に必要という問題があります。

そこで、有限体上で楕円曲線を定義することを考えます。

有限体で定義した楕円曲線なら、扱う数は全て有限体の元なので、
固定長の自然数（ここでは 0 を含む）として扱えるため、
コンピュータで計算するにはうってつけなのです。

「楕円曲線を有限体上で定義する」とはどういうことでしょうか。

楕円曲線の定義は y^2=x^3+ax+b の形の方程式でした。
「ここで出てくる全ての係数、変数が、有限体の元であるとする」
というわけです。

例えば、y は有限体の元なので、y^2 は、
有限体の位数を p としたとき、y^2 \bmod p で計算します。
a も x も有限体の元なので、ax は ax \bmod p で計算します。

これならコンピュータで扱いやすそうですね。

で、今まで有理点にこだわってきた理由ですが、
実は、実数上で定義された楕円曲線の解（つまりグラフの点）の中でも、有理点には、
有限体上で定義された楕円曲線でも対応する点がある、という事実があります。

つまり、今まで有理点について考えてきたお話が、
すべて、有限体上で定義された楕円曲線についても通用するというわけです。

楕円曲線上の有理点について考えることは、
楕円曲線暗号にも役立つ、というわけです。

楕円曲線上の有限巡回群と ECDLP

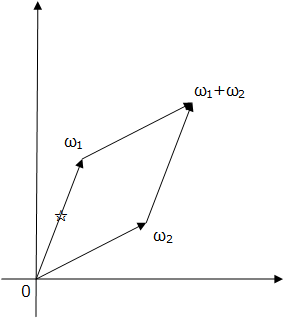
楕円曲線上の有理点は有限巡回群をなす、というお話は前回しました。
これは、有限体上で定義された楕円曲線においても通用します。

楕円曲線のパラメータと、ベースポイントとなる点 G が公開されていて、
秘密の値、x をランダムに決めたとき、G を x 倍した点、P=xG を計算することは簡単です。

愚直に x 回足すと、x のビット数 l に対して最大 2^l-1 回の足し算を行う必要がありますが、
バイナリ法を使えば 2l 回の足し算で済みますから。

じゃあ、逆に、G を何倍かした値 P が与えられたとき、それが G を何倍した値なのか、
つまり、P から秘密の値 x を求めるにはどうするかと言うと、愚直にやって 2^l-1 回の足し算、
もしくは、現在知られているもっと効率の良い方法を使っても、指数関数になる回数の足し算が必要になります。
つまり、「逆は難しい」のです。

この後者でお話した問題、秘密の値 x を求めることを、ECDLP、楕円曲線上の離散対数問題と呼びます。

楕円曲線暗号は、前者が簡単で後者が難しい（現実的な時間で解けない）ことを仮定して設計されています。

まとめ

楕円曲線論を楕円曲線暗号として活用するための最後のピース、
有限体上での定義と、ECDLP についてお話しました。

ここまで連載を読んでいただけた方ならば、
もう、Google や Wikipedia で検索すれば出てくる程度の楕円曲線暗号の解説などは
ある程度読めるだけの基礎知識は身についているものと思います。

なので、これ以上の説明は、その辺の Web サイトや論文等におまかせして、
この連載はそろそろ終了にしようと思います。

みなさん、お付き合いいただき、ありがとうございました。
ご質問、ご意見等ありましたらお気軽にリプライください。
それではまた。

楕円曲線論はじめの一歩 (13)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回は、楕円曲線上の有理点がなす群が、複素平面上の点と準同型な関係にある。
というお話をしました。
今回は、複素平面との関連性から、楕円曲線上の有理点がなす群の性質を探ってみましょう。

位数 3 の点

前回の話の復習になりますが、楕円曲線上の有理点がなす群で、位数が 3 の有理点に対応する点を
複素平面上に図示してみましょう。

f:id:y-hoshizuki:20190122183843p:plain

元々の平行四辺形の格子を、さらに 3 \times 3 に分割した点のいずれか。
その中の、とりあえず 1 つをピックアップしてみました。

この中の、どの点を選んでも、3 倍すると無限遠点に対応する、平行四辺形の頂点にたどり着くことが
確認できると思います。

複素平面上の格子の性質と楕円曲線の性質

今回は 3 \times 3 に分割しましたが、5 \times 5 に分割した場合は
必ず 5 倍すると無限遠点にたどり着きます。10 \times 10 なら 10 倍です。

複素平面上にある点は、必ず、その点で交差する n \times n の格子が存在するため、
どの点であっても、何倍かすれば必ず無限遠点に対応する点までたどり着けることになります。

また、楕円曲線上の有理点は、すべて複素平面上に対応する点があるため、
楕円曲線に戻って考えてみれば、

  1. 楕円曲線上の全ての有理点には、複素平面上に対応する点がある
  2. 複素平面上の全ての点は、平行四辺形をいくつかに区切った格子上にある
  3. 格子上にある点は、何倍かすれば平行四辺形の頂点に達する
  4. 平行四辺形の頂点は無限遠点に対応する

という４段を踏まえると、「楕円曲線上の有理点は何倍かすると無限遠点に達する」わけです。

無限遠点は、楕円曲線上の有理点のなす群の単位元でした。
何倍かすると単位元に戻る、ということは、最初の方でお話した時計の短針、あれと同じ構造なわけです。

f:id:y-hoshizuki:20181225191622p:plain

これは 12 倍すると単位元に戻る例でした。

ということはつまり、楕円曲線上の有理点のなす群は、有限巡回群であることがわかります。

言い換えれば、楕円曲線から有理点を 1 つ、適当に選び出すと、
その点を何度も足し続けると、いつかは無限遠点にたどり着くわけです。

まとめ

今回は、楕円曲線上の有理点のなす群は、実は有限巡回群だった、というお話でした。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。

楕円曲線論はじめの一歩 (12)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回、楕円曲線上の有理点は、可換群であるというお話をしました。
可換群であるということがわかると、次に気になるのはその位数や構造です。

今回は楕円曲線上の有理点がなす可換群の構造について見ていきましょう。

今回の話は、私が楕円曲線について勉強したとき、
「これすごくない！？」と感動したところなので、
この感動をぜひ皆さんとも共有したく思います。

正直に言うと、この話が書きたくて、この連載をしていると言っても過言ではないくらいです。

楕円曲線上の有理点がなす可換群と、複素平面との、切っても切れない関係

昔むかし、ヴァイエルシュトラスさんが発見しました。

楕円曲線 y^2=x^3+ax+b の係数、a と b から上手いこと計算すると、
複素数 \omega_1 と \omega_2 を求めることができます。

この 2 点を複素平面上に置きます。

f:id:y-hoshizuki:20181225193938p:plain

すると、0 と \omega_1、\omega_2、\omega_1+\omega_2 の 4 点で
平行四辺形を作ることができます。

ヴァイエルシュトラスさんは、この平行四辺形の中の複素数と、
楕円曲線上の有理点がなす可換群が一対一で対応づけできる。
ということを発見しました。

これだけじゃピンとこないと思うので、具体例をあげていきたいと思います。

無限遠点と対応する複素数

\omega_1 と \omega_2 を整数個足した点を図示してみましょう。

f:id:y-hoshizuki:20181225193954p:plain

こんな感じに、平行四辺形がたくさんできます。

この平行四辺形の交点、すべてが、無限遠点と対応付けられる複素数です。

位数 2 の点と対応する複素数

楕円曲線上の有理点の個数は未解決問題なので、
可換群の「群の位数」は不明です。

ですが、「元の位数」ならわかるものはいくつかあります。

f:id:y-hoshizuki:20181225194008p:plain

例えばここ。x 軸との交点。P と名づけましょう。

ここが有理点の場合、傾きは垂直なので、
接線は当然、垂直線になります。

ということは、P+P=\mathbb{O} と無限遠点になるため、

P P
P+P O
P+P+P P
P+P+P+P O

というわけで、元の位数が 2 の有理点であることがわかります。

さて、複素平面に戻りましょう。

f:id:y-hoshizuki:20181225194022p:plain

☆マークを打ちました、\frac{\omega_1}{2} の点が、有理点 P と対応します。

先ほどお話した通り、有理点 P の「元の位数」は 2 だったので、
P+P=\mathbb{O}
でした。

複素平面で対応する点を計算してみましょう。
\frac{\omega_1}{2}+\frac{\omega_1}{2}=\omega_1
はい、平行四辺形の交点にたどり着きました。

どうでしょう？
2 倍すると無限遠点になる有理点 P と対応する複素数 \frac{\omega_1}{2} も、
2 倍することで無限遠点と対応する複素数 \omega_1 になるわけです。

楕円曲線上の有理点と、複素平面上の点とが対応しているだけでなく、
「楕円曲線上の有理点の加算は、複素数の加算と対応している」ことがわかるでしょうか？

今回は元の位数が 2 の点で試しましたが、他の位数の点でやっても、
同じようなことが言えます。

これ、すごくないですか？
すごいですよね？？

楕円曲線上の有理点と複素平面上の点（複素数）とが対応しているだけではなく、
有理点同士の加算と、複素数の加算がちゃんと対応しているというわけで、
この 2 つの群は本質的に同じ構造を持っている、という主張ができるわけです。

端的に言ってすごいと思います。

まとめ

「楕円曲線上の有理点からなる群」という世界と、「複素平面」という世界。
2 つの世界がつながっているというお話でした。

それぞれの世界の元同士が対応していて、演算も対応したものが存在している。
このような関係を、専門用語で「準同型」と呼びます。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。

楕円曲線論はじめの一歩 (11)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回までで、楕円曲線上にある 1 つか 2 つの有理点から、
異なる有理点を見つける、という作業についてみてきました。

今回は、その作業についてもう少し詳しく考えてみましょう。

「新たな点を見つける」という演算

与えられた楕円曲線と、2 つの有理点から、異なる有理点を導き出す操作。

りんごが 1 個（点 P）と、別のりんごが 1 個（点 Q）から、りんごが 2 個ある状態（点 S）を導き出すのと
まったく同じ構図であることに、気づいたでしょうか？

そう、P と Q から S を求める。これもまた、足し算と同じ「演算」と呼べるのです。

点と点を足し算する演算、つまり「群」であるわけです。

群であることを確かめてみましょう。

演算が閉じている

線を引いて交点を求めるので、演算については閉じていることがわかります。
もちろん、無限遠点を含めれば、の話ですが。

結合法則

これを証明するのは少々大変なので省略しますが、
結合法則も実はちゃんと満たします。

単位元は無限遠点

無限遠点と楕円曲線上の点との足し算は、元の点のままになります。

逆元は x 軸に対して対称な点

前回お話した通り、( x, y ) と ( x, -y ) を足すと無限遠点になります。

つまり、点 P ( x, y ) と点 -P ( x, -y ) の足し算は単位元になるわけで、
( x, y ) と ( x, -y ) は逆元の関係にあることがわかります。

可換群である

2 つの点を通る直線を引く、という操作から始まるので、
どちらがどちらでも結果は変わらないことはお分かりと思います。

つまり、この群は可換群といえます。

まとめ

いかがでしたでしょうか。
楕円曲線上の有理点について調べると、
実は可換群であったことがわかりました。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。

楕円曲線論はじめの一歩 (10)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回は、楕円曲線と直線が 2 点で交わる場合について見てみました。
実はもう 1 パターン、2 点でしか交わらないケースがあるので、
今回はそちらについて見てみましょう。

垂直線になる場合

f:id:y-hoshizuki:20181225193558p:plain

これはつまり、( x, y ) と ( x, -y ) が与えられた場合ですね。
この場合は完全な垂直線を引くことになり、2 点でしか交わりません。

そこで、「無限遠点」という概念を持ってきます。

f:id:y-hoshizuki:20181225193614p:plain

グラフの上の方（下の方でもいいですが）には、「全ての垂直線と交わる点がある」と考えます。

少し突飛な考え方ですね。

地球儀の、北極点を想像してみてください。
北極点は、地球上の全ての経度線と交わっていますね。
そんな感じです。

二次元のグラフで見ていると少し滅茶苦茶に見えますが、
実は射影平面という考え方を導入して三次元で見ると実在する点なのです。

射影平面

ここで、楕円曲線の定義を思い出してみましょう。

y^2=x^3+ax+b

ここで、今は有理点、つまり x と y が有理数である点について考えているので、
有理数は 2 つの整数を使って \frac{X}{Z} と表すことができるため、

\frac{Y}{Z}^2=\frac{X}{Z}^3+a\frac{X}{Z}+b

と書くことが出来ます。大文字で書いた X, Y, Z は全て整数です。

両辺に Z^3 をかけてやると、

Y^2Z=X^3+aXZ^2+bZ^3

となります。どの項も、X, Y, Z をあわせると 3 次の項になっていることがお分かりでしょうか？
a と b は楕円曲線を定義するパラメータで、定数なので次数にはカウントしません。

このように、全ての項の次数が同じ方程式のことを、同次式と呼びます。

変数が 3 つに増えたので、三次元のグラフを想像してみましょう。

f:id:y-hoshizuki:20181225193627p:plain

このように、3 次元の空間でみると、Z=1 のところでスライスした断面図が、
今まで見てきた楕円曲線のグラフであることは、数式からわかると思います。

次元が 1 つあがっているので、楕円曲線上の点は、この空間内での線（実際には「整数」に限定してるので点線）
になり、楕円曲線自体は面（整数に限定してるのでメッシュ状の面）に対応していることになります。

2 つの点を結ぶ直線も面に対応しているので、楕円曲線の面と重なっている曲線が、交点を表すことになります。

では無限遠点はどこに対応するのでしょうか？

f:id:y-hoshizuki:20181225193642p:plain

それはここ。Z=0 の平面です。

グラフ上でどの垂直線をとっても、この三次元空間で見ると Z=0 の面と交差していることにします。

というわけで、二次元では描けない点が実は存在している、ということで
理解しておいていただければと思います。

ちなみに、無限遠点は \mathbb{O} と表記することが多いようです。

まとめ

今回は、楕円曲線と直線が 3 点で交わらないケースの最後の 1 パターンについて見てみました。
射影平面という概念を導入することで、無限遠点というものを手に入れました。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。

楕円曲線論はじめの一歩 (9)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回、「楕円曲線に交わるように直線を引くと、その直線は必ず 3 箇所で交わります」と書きましたが、
実際には例外があります。

今回はその例外について見ていきましょう。

楕円曲線と接する場合

f:id:y-hoshizuki:20181225193413p:plain

楕円曲線に直線を重ねると、この図のように接線となる場合があります。
その場合は、2 点でしか交わりません。

このような場合は、3 点で交わっている状態から連続的に変化させていき、その極限を考えます。

f:id:y-hoshizuki:20181225193426p:plain

P-P'-Q の直線は 3 点で交わっています。
これを少しずつ、Q の位置を変えずに上にずらしていきます。

すると、P と P' はどんどん近づいていって、あるとき P'' の 1 点に集約されます。

つまり、接線となっている点は、その点で 2 回、交わってる状態と「連続」しているわけです。
要するに、接線の部分で 2 回交わっているとカウントするわけですね。

中学校で二次方程式の解を求める時に、「重解は 2 回交わっているものとみなす」と習いました。
あれと同じです。

数式で考えるともう少し明白です。

前回、2 点 P = ( x1, y1 ) と Q = ( x2, y2 ) から有理点 S を求める式をお見せしました。

x_3=(\frac{y_2-y_1}{x_2-x_1})^2-x_1-x_2
y_3=\frac{y_2-y_1}{x_2-x_1}(x_1-x_3)-y_1

ここで、\lim_{x_2 \to x_1} を考えます。
x2 が変化すると y2 もあわせて変化していくことに注意して極限を求めると、

x_3=(\frac{3x_1^2+a}{2y_1})^2-2x_1
y_3=\frac{3x_1^2+a}{2y_1}(x_1-x_3)-y_1

が得られます。今回も詳細な計算は省略します。

式の形はだいぶ違いますが、傾きを表している

\frac{y_2-y_1}{x_2-x_1}

が、

\frac{3x_1^2+a}{2y_1}

に変わっているだけです。

直線を連続的に移動させて点 P と点 P' が極限まで近づいて点 P'' になる。
これを数式で考えるとこうなる、というお話です。

接する場合を考えると何ができるか

さて、以上の考え方を逆にすれば、
「楕円曲線上に有理点が 1 個があれば、そこに接線を引くことで別の有理点が見つかる」
ということになります。

P と P' から S を発見できるのであれば、P'' と P'' からも S を発見できるというわけです。

前回は有理点が 2 個から別の点を見つけましたが、実は 1 個でもあれば見つけられる、
というお話です。

まとめ

今回は、楕円曲線と直線が 3 点で交わらないケースについて見てみました。
実はもう 1 パターンあるのですが、それについては次回、触れることにしましょう。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。

楕円曲線論はじめの一歩 (8)

今回のおはなし

みなさんこんにちは。

VIPPOOL でエンジニアをやっています、星月です。

前回まで、代数論の基礎を簡単になぞりました。
そして今回からみなさんお待ちかね、楕円曲線の話をはじめようと思います。

そもそも楕円曲線とは

楕円曲線って何でしょう？

楕円曲線とは、y^2=x^3+ax+b こんな形をした方程式のことです。

a, b は係数で、x と y が変数です。
この方程式の解をグラフにするとこんな感じになります。

f:id:y-hoshizuki:20181225193049p:plain

f:id:y-hoshizuki:20181225193102p:plain

え、どのあたりが楕円かって？...名前のことは気にしない方がいいです。
いろいろな歴史的事情でこう呼ばれているだけで、これが楕円曲線なんです。

詳しく知りたい方は、楕円積分について調べるといいですが、
あまりオススメはしません...

天下り的で申し訳ないですが、こればかりは、「こういうもの」として
覚えていただければと思います。

楕円曲線上の有理点

さて、問題です。

ある楕円曲線が与えられたとき、その楕円曲線に含まれる有理点、
つまり x, y 座標それぞれが有理数となる点はどれだけあるでしょうか？

まったく存在しない？それとも有限個？もしくは無限に存在する？

...実はこの問題は未解決問題の 1 つで、未だに回答は出ていません。
残念。

楕円曲線上の有理点を探す問題

未解決の問題について考えても仕方ないので、
とりあえず、さらに条件を加えます。

ある楕円曲線と、「その楕円曲線上の有理点が 2 つ与えられたとき」、
他の有理点を探すことはできるでしょうか？

f:id:y-hoshizuki:20181225193119p:plain

実は、楕円曲線に交わるように直線を引くと、その直線は必ず 3 箇所で交わります。
実際には例外があって 2 箇所になる場合もありますが、とりあえず後回しにします。

この交点を左から順に P, Q, R としましょう。
P と Q が有理点であれば、R も有理点になることは計算すればわかります。

これだけだと、3 つ目を見つけて終了してしまいますので、さらにもう 1 つみつけましょう。

f:id:y-hoshizuki:20181225193205p:plain

R を通る垂直線との交点、つまり、R の y 座標を反転させた点 S も有理点となります。
( x, y ) が有理点なら、 ( x, -y ) も有理点、という話です。

さて、これで 4 つ目が出てきました。ここで、直線 SP や直線 SQ を引くと、
さらにたくさん有理点が見つかりそうですね。

点 S を導き出せるのは非常に重要そうです。

さて、ここで、つまり有理点は無限に存在するんだ！と思ったあなた、残念早とちり。
これを繰り返したときに、既知の点以外である保証がないので、
無限に存在するとは限りません。つまり、どこかでループする可能性があるのです。

ともあれ、2 つの有理点から、別の有理点を見つける方法があることはわかっていただけたと思います。

実際に計算してみる

有理点 P の座標 ( x1, y1 ) と、有理点 Q の座標 ( x2, y2 ) から、新たな有理点 S の座標 ( x3, y3 )
を求めてみましょう。

詳しい計算については他のサイトを参照してもらうことにしてここでは答えだけ。

x_3=(\frac{y_2-y_1}{x_2-x_1})^2-x_1-x_2
y_3=\frac{y_2-y_1}{x_2-x_1}(x_1-x_3)-y_1

と、なります。x1, x2, y1, y2 すべて有理数ならば、x3, y3 も有理数になることがおわかりでしょうか？

有理点 2 つから、新たな有理点が得られることが、数式からも見て取れます。

まとめ

今回からようやく楕円曲線の話に入りました。
話題の焦点は「楕円曲線上で、x と y がともに有理数となる点」つまり「有理点」です。
これを突き詰めていくと面白いことがたくさんあります。

今回はここまで。
ご質問、ご意見等ありましたらお気軽にリプライください。